Roughly in order of interest. There are other things of interest but these are just possible projects/vague directions i could identify
Upper Critical Dimension (UCD) for Mean Field Rheological Models
Background
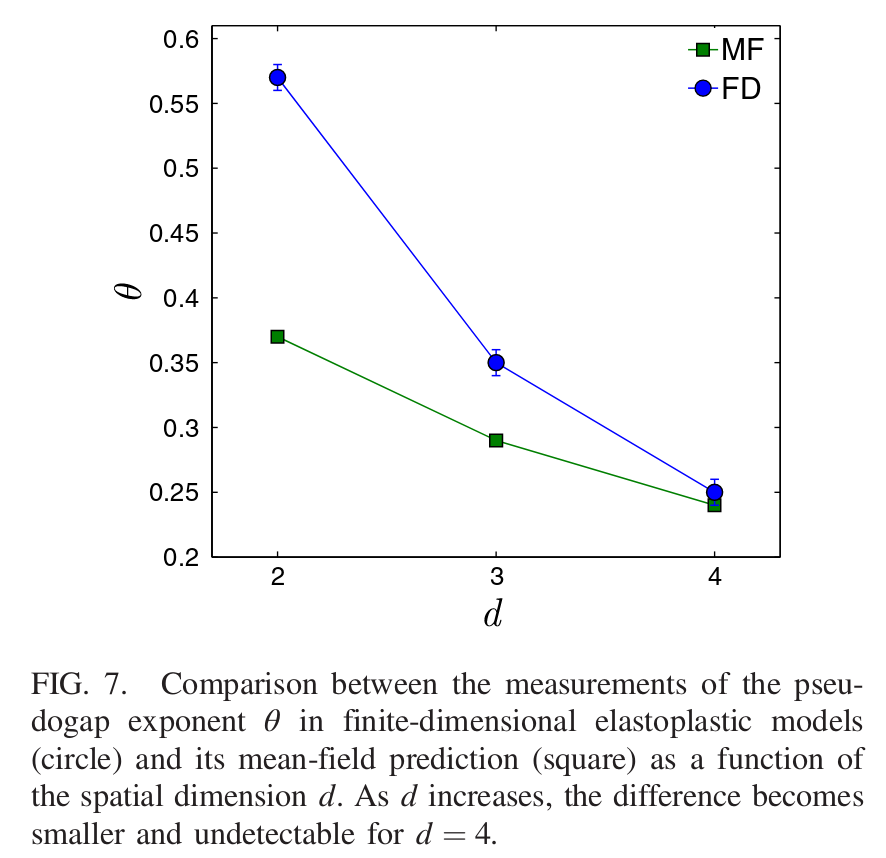
- Jie Lin and Wyart published Mean Field Description of Plastic Flow in Amorphous Solids , where they calculated an exponent \(\theta\) that characterises the density of regions that flow plastically under small shear stress ( \(P(x) \approx x^{\theta} )\). They calculate the exponent by using a broadly distributed noise term corresponding to the statistics of Levy flights. Their \(\theta\) starts to agree well with simulation for \(d=4\) (and greater, I assume) which is weak evidencefor it being the lower critical dimension \(d_c\). They mention that they no Ginzburg-like argument is known for why \(d=4\) is relevant.
- Model: discrete sites with stress values with rules for redistribution. \(x_j \equiv 1 - \sigma_i\) where \(\sigma_i\) is the stress on site \(i\). Update rules are:
Directions
- Development of Ginzburg argument. Criterion typically derived by considering fluctuations about the mean field bahviour starting from a free energy, but no free energy here. Effective one such as from a LD principle? Gaussian mixture modelling of the noise to replicate broad tail? Something analogous to dynamical RG? if possible dimensional expansions for exponents when \(d < d_c\). Could possibly link to other MF glass/rheological models (such as HL-model or Zamponi’s infinte dimensional glasses, where there are also no Ginzburg like arguments or dimensional expansions)
Memory and Resets with Large Deviations
Background
-
There is a lot of unconnected work to do with memory effects in various stochastic systems. The most comprehensive work I’ve seen is by Christian Maez in Fluctuation-response relations for Nonequilibrium Diffusions with Memory where they consider linear underdamped langevin equations with a memory kernel on the velocity damping term. In addition there has been some work to do with breaking detailed balance without introducing memory (Fodor, Hayakawa, Tallier, Wijland)
-
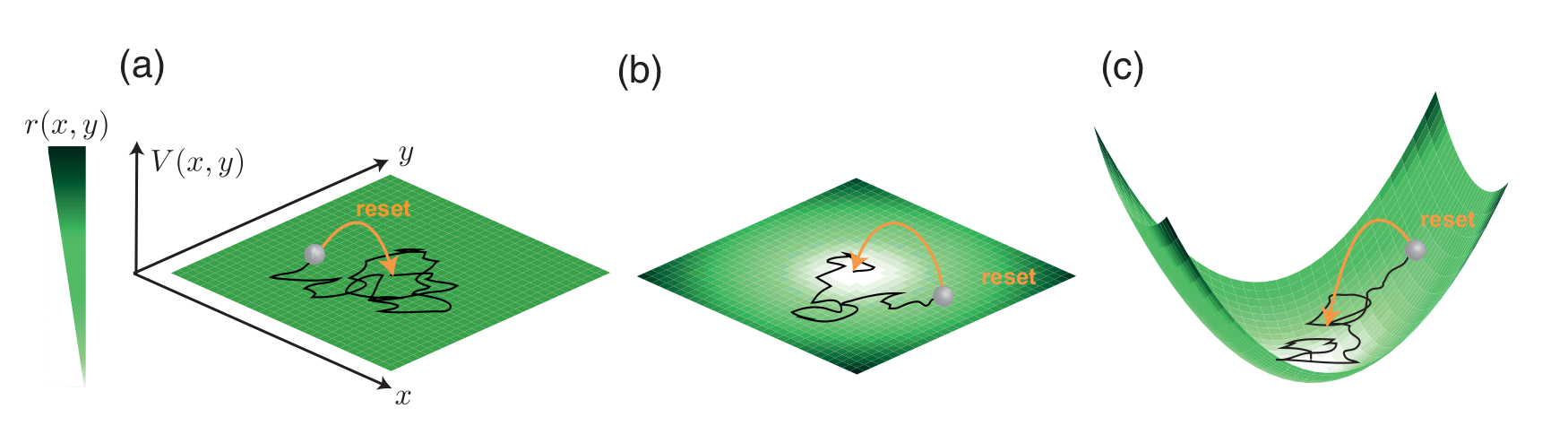
Harris and Touchette studied how discrete time stochastic resetting can lead to dynamical phase transitions (of both orders). They looked at particular model with uniform resets, but have left out the continuum case, space-time dependent resetting rates etc and mention this as an interesting future direction
Directions
- Calculation of large deviation behaviour of space-time dependent resets for brownian particles. There is already a recent path integral formalism to deal with space dependent resets, so it may be relatively straightforward to apply large deviation biases analytically as well as computationally determine qualitative features of Large devitaion transitions in such systems. For a particle moving in a 1D potential \(V(x)\) and with a spatially varying reset rate $r(x)$ the probability of no reset is
And biased probability distributions take the form \(P_{bias} \propto e^{-\lambda A} P_{\text{n_reset}}\). Would reduce to a hermitian quantum problem (as in the Touchette paper ) and may be able to say something about optimalling resetting choice for some defined escape times, confinement etc etc
"Odd Elasticity"
Background
- Vincenzo Vitelli has done preliminary work on the mechanics of elastic materials which exhibit “odd elasticity”. This means that the tensor relatin stress and strain via \(\sigma_{ij} = K_{ijmn} \epsilon_{mn}\) is not even under the reversal of the first two and second two indices, but is in fact odd i.e \(K_{ijmn} = - K_{mnij}\). This difference to the normal symmetry can be related to active units within the materials in question, which are being experimentally realised. To my understanding, the elastic theory of such materials has basically never been studied.
Directions
- Work extraction properties of these elastic materials (although VV has some unpublished work on this in progress)
- Elastic wave propogation, stability analyses, dislocations, thermal properties i.e all the basic analysis but for systems with this new symmetry